оптимальной точностью и затратами, уменьшения или выделении ошибки экспериментальных исследований, возможности принятия решений на основе формализованных правил, оптимизации воздействий в тренировочном процессе для достижения реальных результатов в заданное время.
Представим организм футболиста в виде вектора исходных состояний Z = (Z1, Z2, ... Zi,... Zn), подтвержденных с определенной точностью задаваемых вектором влияющих факторов X = (Х1-Х2...Х...ХП) с (последующей реакцией измеряемых параметров Y = (Y1-Y2, ... Yj ... Yn). Задача состоит в том, чтобы на основании экспериментальных данных каждого параметра определить функцию
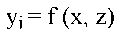 (1)
(1)
с определенной точностью аппроксимирующую процесс. Это возможно с использованием теории планирования эксперимента.
Планом эксперимента называется некоторая матрица F (X, Z), строки которой содержат значение факторов и исходных состояний в опыте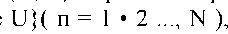 а
а
столбцы — значение фактора Xi для исходного состояния Zi в N опытах. В зависимости от свойства плана эксперимента можно получить полином ( уравнение регрессии) различного порядка: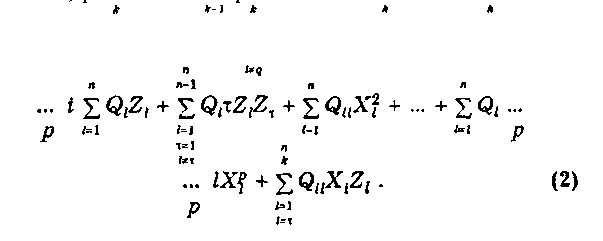
где Q0, Qi, Qii, ..., Qi.i — коэффициенты уравнения регрессии нулевого, первого, второго и т.д. порядка соответственно;
Qij — коэффициент уравнения регрессии для эффекторов взаимодействия факторов Х1пХ аналогичного коэффициента уравнения регрессии для исходных состояний;
Qi,- — коэффициент уравнения регрессии для взаимодействия факторов Xi и исходного состояния Zi.
Задача нахождения коэффициентов уравнения регрессии решается методом наибольших квадратов или в матричной форме:
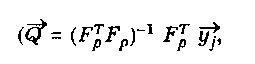
где
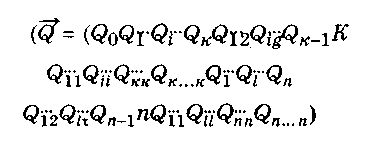
где — Fp расширенная матрица плана эксперимента размера