Для примера остановимся на некоторых из них:
Z i — сократительная способность мышц (ССМ);
Z 2 — сопротивляемость мышц утомлению (СМУ);
Zз — ускорение общего центра массы (q).
Состояние указанных параметров оценивалось до воздействий и после выполнения серий игровых упражнений в восстановительном периоде (t0 = О, t1 = 2, t2 = 24, t3 = 30, t4 = 48, tb = 72 ч отдыха).
В качестве параметров математических моделей использованы те же управляемые системы, но после тренирующих воздействий, которые обозначим: у1
— ССМ; у2 — СМУ; у^ = q.
В силу того, что влияющие факторы и .исходные состояния варьируют в различных диапазонах величин и имеют разные размерности, при матемаатическом моделировании производили их нормирование на интервале (-1, 1) по правилу :
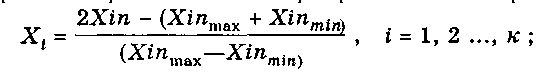
где Xi — нормирование значения фактора;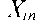
— натуральное значение
фактора;— соответственно максимальное и минимальное значение
фактора.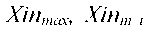
Аналогично проводили нормирование вектора Z:
В математических моделях, таким образом, присутствуют только нормированные значения факторов и исходных состояний.
Вычисления коэффициентов регрессии, анализ их значимости и адекватности математическим моделям проводили с помощью программы
В результате получены математические модели, адекватно описывающие влияние тренирующих воздействий и исходных состояний с вероятностью до 97,5%.
С помощью уравнения регрессии для различных стадий восстановительного периода находили оптимальные воздействия при заданных исходных состояниях для каждого параметра в отдельности и общего критерия параметров, используя программу оптимизации Simnel на ЭВМ ЕС 1020.
Изложенная выше и апробированная в условиях практики методика моделирования и поиска оптимальных тренирующих воздействий показала, что возможен строго формализованный выбор оптимальных соотношений количественных сторон функциональных биологических систем. При этом оказалось возможным создание необходимых состояний в заданное время расчетным путём с учетом временной адаптации (срочной и отдаленной).
Как было определено, алгоритм воздействия типа "А" (табл.1) создает соотношение функциональной активности систем, способствующее развитию разных.сторон специальной выносливости (в зависимости от применяемых средств
— скоростной, силовой или координационной выносливости).
